Filters, and what are high-speed filters?

Filters are great for astrophotography. They work by blocking out colours (that is, frequencies of light) that you don’t want. The images you get when you use a filter are made up of the frequencies they let through.

Filters can’t, of course, enhance or amplify any frequencies, but by blocking out unwanted light you can push the colours you do want. To quote Blackadder, “the effect is much the same”.

Here’s an example: it’s the same area of the sky, Fenrir, the Dark Wolf. These are one without and one with a filter. The difference is, like the nebula itself, quite dramatic. The filter closes in on 656.3 nanometres, which known as “Hydrogen alpha”. Of course, because the filter removes light rather than adding it, the exposure length on the second image is longer than the first image.

Frequency response graphs

Now we know what filters can do, we can start to describe them in more technical ways. I’ll keep talking about Hydrogen alpha, which centres on 656.3nm (which is the frequency that is emitted by ionised hydrogen).

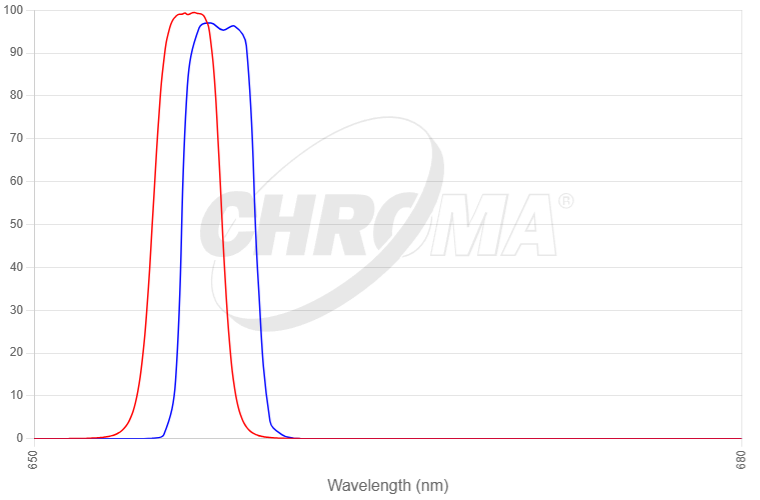
For every frequency, we can graph the amount of light that successfully passes through the filter.  We call this a frequency response curve, and filters should all have one of these. The two lines on the graph below show two Hydrogen alpha (Ha) filters, and both centre on our magic 656.3nm. As you can see, the filter with the blue line filters out less light as it cuts out light below about 654 and above about 659nm. The one with the red line cuts out more, just letting in light between 655 and 658nm. We call this range the “bandwidth”, and the blue line is for a Ha filter with 5nm bandwidth, with the red line being for a filter with a narrower, 3nm bandwidth.

Why is a narrow bandpass better?

There are a couple of differences between the two filters with different bandwidths. First, because more light comes through the filter with the wider bandwidth, you can either take a shorter image to get the same overall look, or you can use the same exposure to get a brighter image.

More importantly though, with the narrower bandwidth filter you get rid of more of the light you don’t want. Because this light is either unwanted noise, or from other elements in the nebula, this means the image will be cleaner and sharper, especially around the edges of structures in the nebula – these are often associated with shockwaves which shape the overall view. The narrower the bandpass, the sharper and cleaner your image will be, even if you need more data for the final image.

Always good, right? Yeah, well, it’s complicated.

What happens with a fast scope and narrow bandpass?

Telescopes come with different apertures and focal lengths. A telescope’s “speed”, or focal ratio, determines how bright the telescope will be. Generally, telescopes with a lower focal ratio (that is, ones that have a large aperture and short focal length – let’s say short fat ones) need shorter exposures for the same overall image. Long thin telescopes (with a high focal ratio) need longer exposures.

But it’s not all great for short fat telescopes. Thinking of their geometry, light that comes from the edge of the lens will hit the camera sensor at a higher angle than a long thin telescope. This suddenly becomes a problem for filters. Because light coming in at a high angle changes its frequency. The faster the focal ratio, the shorter the wavelength that is transmitted through the filter.

So here’s the problem

Let me explain. You only want Fenrir’s Hydrogen alpha light, which is at 656.3nm, and you’ve chosen an expensive filter with a 3nm bandwidth, which lets light in between 654.8 and 657.8nm. To make things faster, you’re using a RASA as your telescope, which has a blindingly fast focal ratio of about 2. This super high-speed scope will cause a spectral shift such that your filter only lets through light between 653 and 656nm. The effect is that you end up filtering OUT the light you want and letting IN the light you don’t want!

How can we solve this?

As you can see, this is a serious problem. Could it be that the more expensive your equipment is, the less likely it is to get the details in the nebula you want?

What can you do to get your filter to give you the right frequency?

Widen the bandpass

The first (and cheapest) solution for users of fast telescopes is to get a filter with a wider bandpass. Widening your window to 5nm or even 7nm will guarantee that all the Hydrogen alpha light passes through to your sensor. The problem is that a bunch of scattered noisy light will get through as well, softening your image and confusing details in the nebula with those created by other elements.

Shift the bandpass window

Here’s the solution we’ve been building to. You can get narrow bandwidth filters that are especially made for high-speed telescopes. These allow light through with a shorter wavelength – knowing that you’re going to be using it on a telescope that causes the frequency shift.

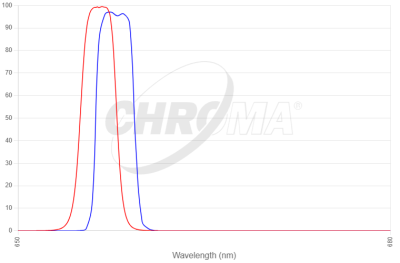
Here’s the frequency response curves of two Ha filters, both of which have 3nm bandwidth. The normal filter (that’s the red line) allows light of 656.3nm (plus or minus 1.5nm). However, the “high speed” filter (the blue line) allows light of a slightly longer wavelength through (about 658nm). The angle of the light hitting the filter will shift this back down to the right frequency, meaning your precious Hydrogen alpha light gets through – and nearly nothing else.

For narrowband filter sets, the same type of shift applies to the Oiii and Sii filters.

The result?

If you’re using a telescope of f/4 and above (that’s me), you don’t have to worry about all this. Similarly, if you are using fairly broad bandwidth filters (mine are 7nm) this also doesn’t apply to you.

However, if you want to use paricularly narrow bandwidth filters, your choice is a little more nuanced.

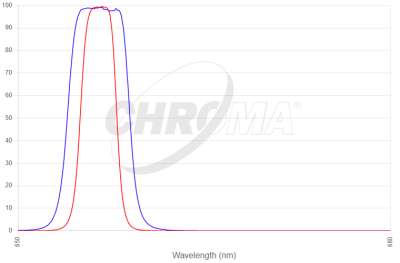
If your optical system has a focal ratio of above around f/4, your filters don’t need the shifted frequencies, such as these ones.

If your system is especially fast, below f/3, your filters will need the shifted frequencies, such as these ones.